Matematika 2 - 6.1 Logaritamska funkcija

Logaritam

Spoji jednadžbe s pripadnim rješenjima.

$x + 2 = 4$	$x = 2^{2}$
$2^{x} = 8$	$x = ?$
$\sqrt{x} = 2$	$x = 4 : 2$
$2 x = 4$	$x = 4 - 2$

null

Za rješavanje jednadžbi tipa

2^{x} = 8

potrebna nam je neka inverzna radnja (funkcija) koja će poništiti bazu potencije (eksponencijalnu funkciju). Ta radnja naziva se logaritam.

Logaritam po pozitivnoj bazi ( $a \neq 1$ ) od nekog pozitivnog broja $y$ označavamo $\log_{a} y,$ a čitamo "logaritam broja $y$ po bazi $a$ ". To je jedinstveni eksponent $x,$ kojim treba potencirati bazu $a$ da bi se dobilo $y.$ Matematički zapisano: $\log_{a} y = x \Leftrightarrow a^{x} = y .$

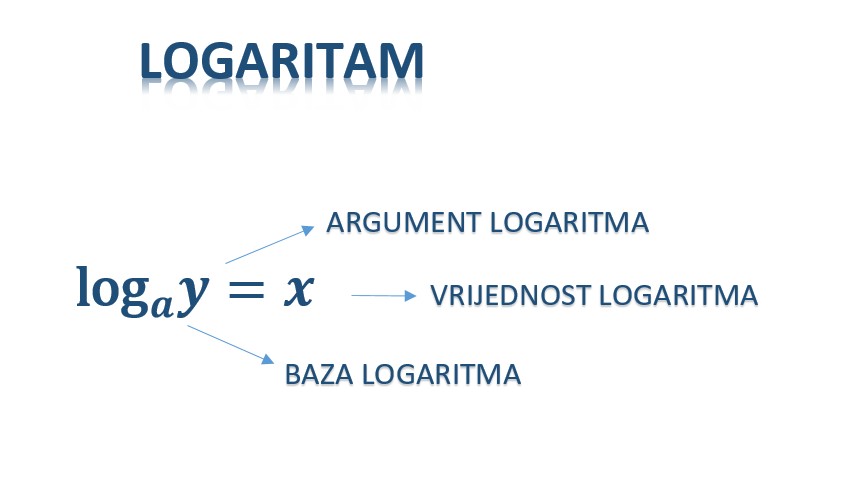
Pripazite na zapisivanje logaritama. Oznaka za logaritam $\log$ piše se u istoj ravnini kao i argument logaritma $y$ i vrijednost logaritma $x,$ dok je baza $a$ indeks i piše se spušteno, manje veličine.

Primjer 1.

$\log_{2} 8 = 3 \Leftrightarrow 2^{3} = 8$

$\log_{3} 81 = 4 \Leftrightarrow 3^{4} = 81$

$\log_{2} \sqrt{2} = \frac{1}{2} \Leftrightarrow 2^{\frac{1}{2}} = \sqrt{2}$

$\log_{4} 1 = 0 \Leftrightarrow 4^{0} = 1$

Spojite ekvivalentne jednakosti.

$\sqrt{49} = 7$	$3^{3} = 27$
$\log_{3} 27 = 3$	$\log_{49} 7 = \frac{1}{2}$
$8^{2} = 64$	$8^{- 1} = \frac{1}{8}$
$\log_{8} (\frac{1}{8}) = - 1$	$\log_{8} 64 = 2$

null

Spojite ekvivalentne jednadžbe.

$\log_{M} N = b$	$M^{b} = N$
$b^{M} = N$	$b^{N} = M$
$M^{N} = x$	$\log_{b} N = M$
$\log_{b} M = N$	$\log_{M} x = N$

null

Da biste odredili logaritam nekog broja, možete taj broj napisati kao potenciju s bazom koja je ujedno i baza logaritma. Logaritam je tada eksponent te potencije.

"Logaritam je eksponent, to svatko zna!"

Primjer 2.

$\log_{2} 16 = \log_{2} 2^{4} = 4$

$\log_{5} 5 = \log_{5} 5^{1} = 1$

$\log_{4} 2 = \log_{4} 4^{\frac{1}{2}} = \frac{1}{2}$

$\log_{\frac{1}{5}} 25 = \log_{\frac{1}{5}} {(\frac{1}{5})}^{- 2} = - 2$

Zadatak 1.

Odredite vrijednosti logaritama.

$\log_{2} 32 =$
$\log_{5} 25 =$
$\log_{3} (\frac{1}{9}) =$
$\log_{9} 3 =$

null

Kod definicije logaritama naveli smo da baza mora biti pozitivna i različita od $1 .$

Što bi se dogodilo da je baza negativna?

Kad bi baza bila npr.

- 2

i logaritam

\frac{1}{2}

, tj

\log_{- 2} x = \frac{1}{2},

ne postoji realan broj

x

za koji vrijedi

{(- 2)}^{\frac{1}{2}} = x .

Kad bi baza bila

1,

računajući

\log_{1} 5 = x

dobili bismo

1^{x} = 5

,

što je nemoguće (ne postoji

x

za koji je

1^{x} = 5

Kako je vrijednost potencije s pozitivnom bazom različitom od

1

uvijek pozitivna, nije moguće odrediti logaritam od negativnog broja ili nule.

Zadatak 2.

Izračunajte:

$\log_{3} 27 =$
$\log_{25} 5 =$
$\log_{7} \frac{1}{49} =$
$\log_{9} \frac{1}{3} =$

$\log_{3} 27 = 3$
$\log_{25} 5 = \frac{1}{2}$
$\log_{7} \frac{1}{49} = - 2$
$\log_{9} \frac{1}{3} = - \frac{1}{2}$

Iz definicije logaritama slijedi da sve što je zapisano s pomoću logaritama možemo napisati s pomoću potencija, i obrnuto: sve što je napisano s pomoću potencija možemo zapisati s pomoću logaritama.

ELIMINACIJA LOGARITAMA

$\log_{a} y = x \Rightarrow y = a^{x}$

$\log_{a} a^{x} = x$

ELIMINACIJA POTENCIJE

$a^{x} = y \Rightarrow x = \log_{a} y$

$a^{\log_{a} y} = y$

Zadatak 3.

Odredite vrijednost izraza:

$5^{\log_{5} 7} =$

$\log_{5} 125 =$

$\log_{x} x^{9} =$

$3^{1 + \log_{3} 7} =$

$5^{\log_{5} 7} = 7$

$\log_{5} 125 = \log_{5} 5^{3} = 3$

$\log_{x} x^{9} = 9$

$3^{1 + \log_{3} 7} = 3^{1} \cdot 3^{\log_{3} 7} = 3 \cdot 7 = 21$

Zanimljivost

Logaritmi su naziv dobili od škotskog matematičara Johna Napiera (1550.-1617.).

Riječ logaritam dolazi iz grčkog jezika, od dviju riječi: logos, što znači računanje, i arithmos, što znači broj. Napier je mislio kako će otkriće logaritama ubrzati računanje s velikim brojevima.

U njegovo doba to je bila velika korist astronomima, koji su bez upotrebe kalkulatora ili računala trebali računati s vrlo velikim brojevima. Stoga je francuski matematičar Pierre Laplace (1749. - 1833.) izjavio da je Napier "udvostručio život astronoma".

Kako poznavanje logaritama može ubrzati računanje s velikim brojevima, vidjet ćete u jedinici 6.4 Računanje s logaritmima.

Zadatak 4.

Poredajte vrijednosti navedenih izraza po veličini, od manje prema većoj.

$\log_{2} 4$
$\log_{2} (\frac{1}{4})$
$\log_{2} 2$
$\log_{2} 1$
$\log_{2} (\frac{1}{2})$

null

Izračunajmo $\log_{2} 3 .$

Broj $3$ se ne može prikazati kao potencija s bazom $2$ i racionalnim eksponentom.

Znamo da je $\log_{2} 2 = 1$ i $\log_{2} 4 = 2 .$

Zadatak 5.

Vrijednost $\log_{2} 3$ jednaka je $1.5 .$

To bi bilo točno u slučaju linearne ovisnosti. Ova ovisnost nije linearna.

Pomoć:

Prisjeti se potencija i eksponencijalne ovisnosti. Logaritmi su inverzni od potencija.

null

Da bismo odredili vrijednost logaritma $\log_{2} 3,$ možemo upotrijebiti džepno računalo. Tipka koja nam daje mogućnost računanja logaritama izgleda ovako: $\log_{x} y$ ili $\log_{} .$

Vrijednost koju dobijemo računanjem na džepnom računalu je $\log_{2} 3 = 1.584962501 .$

Ako vaše džepno računalo nema takve tipke, ne očajavajte. Pravim matematičarima ona i ne treba (nekad matematičari nisu ni imali džepna računala). Dovoljne su tipke $\log$ ili tipka $\ln .$ Postupak prebacivanja logaritama iz jedne baze u drugu detaljno je prikazan u jedinici 6.4 Računanje s logaritmima.

Dekadski logaritam

Zadatak 6.

Koristeći se džepnim računalom i tipkom $\log$ izračunajte logaritme brojeva $0.01,$ $0.1,$ $1,$ $10,$ $100,$ $1000 .$

$- 2,$ $- 1,$ $0,$ $1,$ $2,$ $3$

Možete li iz rezultata koje ste dobili zaključiti koja bi bila baza logaritma koji nema istaknutu bazu?

(Podsjeća li vas to na drugi korijen? Ipak, baza $\log y$ nije $2 .$ )

Kako već svatko zna da je logaritam eksponent, pogledajmo što smo imali u prethodnom zadatku.

$\log 0.01 = \log 10^{- 2} = - 2$

$\log 0.1 = \log 10^{- 1} = - 1$

$\log 1 = \log 10^{0} = 0 . . .$

Zadatak 7.

Ako baza logaritma nije istaknuta, podrazumijeva se da je baza jednaka:

1

2

10 .

null

Logaritam po bazi $10$ naziva se dekadski ili Briggsov logaritam i označava $\log y .$

Uvijek kad ne spominjemo bazu logaritma, smatramo da je baza $10 .$

Primjer 3.

S pomoću džepnog računala odredimo vrijednosti logaritama brojeva $0.1,$ $0.5,$ $1,$ $2,$ $10,$ $20,$ $200,$ $- 10 .$

$\log 0.1 = - 1$

$\log 0.5 \approx - 0.3$

$\log 1 = 0$

$\log 2 \approx 0.3$

$\log 10 = 1$

$\log 20 \approx 1.3$

$\log 200 \approx 2.3$

$\log (- 10) = M a t h E r r o r$

Pokušajte odrediti logaritam iz još nekih negativnih brojeva ili iz nule (npr. $\log (- 1),$ $\log (- 50),$ $\log 0$ ...).

Razmislite zašto to nije moguće izračunati? Postoji li realan broj koji na neki eksponent daje negativnu vrijednost ili nulu? Poprima li eksponencijalna funkcija negativne vrijednosti? A poprima li nulu?

Prirodni logaritam

Zadatak 8.

Poigrajmo se sada tipkom $\ln$ na vašem džepnom kalkulatoru.

Odredite $\ln$ od brojeva $1,$ $2.718,$ $7.389 .$

$\ln 1 = 0$

$\ln 2.718 \approx 0.99998963$

$\ln 7.389 \approx 1.9999924$

Baza ovog logaritma bila bi približno $2.718,$ što je i približna vrijednost broja $e$ .

$\log_{e} y = \ln y$

Logaritam kojem je baza Eulerov broj, $e,$ naziva se prirodni ili Napierov logaritam i označava $\ln x .$

Zanimljivost

Prirodni ili Napierov logaritam prvi je otkrio John Napier (1550.-1617.), škotski matematičar, fizičar i astronom. Baza mu je Eulerov broj, a može se definirati za sve pozitivne realne brojeve kao površina ispod krivulje $y = \frac{1}{t}$ , u granicama od $1$ do $x .$

Kod najčešće korištenih programskih jezika, uključujući C $,$ C++ $,$ MATLAB, Fortran i BASIC, "log" ili "LOG" označava prirodni logaritam (nije logaritam po bazi $10$ ).

S pomoću džepnog računala odredite vrijednosti prirodnog logaritma brojeva $0.1,$ $1,$ $2,$ $10,$ $- 10 .$

$\ln 0.1 \approx - 2.3026$

$\ln 1 = 0$

$\ln 2 \approx 0.6931$

$\ln 10 \approx 2.3026$

$\ln (- 10) = M a t h E r r o r$

Logaritamska funkcija

Vidjeli smo da je moguće izračunati logaritam bilo kojeg broja većeg od $0 .$ Možemo li sada definirati logaritamsku funkciju?

Logaritamska funkcija po bazi $a$ realna je funkcija oblika $f (x) = \log_{a} x,$ gdje je $a > 0$ i $a \neq 0,$ a domena je skup pozitivnih realnih brojeva.

Logaritamska funkcija je realna funkcija, ali ipak ima neka ograničenja. Za $x$ možemo uzeti samo pozitivne realne brojeve, a vrijednosti logaritamske funkcije će biti svi realni brojevi (čak i $0$ i negativni realni brojevi).

Kako je logaritam inverzna radnja od potencije, onda je i logaritamska funkcija inverzna funkcija od eksponencijalne. Prisjetite se svojstava i grafičkog prikaza eksponencijalne funkcije pa razmislite koja bi svojstva imala logaritamska funkcija i kakav bi bio njezin graf.

Više o grafu logaritamske funkcije i njezinim svojstvima istražit ćete u idućoj jedinici.

Kolekcija zadataka 1

Zadatak 9.

Odredite vrijednosti logritamske funkcije $f (x) = \log_{2} x$ ako su vrijednosti od $x :$ $0.25,$ $0.5,$ $1,$ $2,$ $4 .$

$f (0.25) = \log_{2} 0.25 = \log_{2} 2^{- 2} = - 2$

$f (0.5) = \log_{2} 0.5 = \log_{2} 2^{- 1} = - 1$

$f (1) = \log_{2} 1 = \log_{2} 2^{0} = 0$

$f (2) = \log_{2} 2 = \log_{2} 2^{1} = 1$

$f (4) = \log_{2} 4 = \log_{2} 2^{2} = 2$

Zadatak 10.

Odredite vrijednosti logritamske funkcije $f (x) = \log_{\frac{1}{2}} x$ ako su vrijednosti od $x :$ $0.25,$ $0.5,$ $1,$ $2,$ $4 .$

$f (0.25) = \log_{\frac{1}{2}} 0.25 = \log_{\frac{1}{2}} {(\frac{1}{2})}^{2} = 2$

$f (0.5) = \log_{\frac{1}{2}} 0.5 = \log_{\frac{1}{2}} \frac{1}{2} = 1$

$f (1) = \log_{\frac{1}{2}} 1 = \log_{\frac{1}{2}} {(\frac{1}{2})}^{0} = 0$

$f (2) = \log_{\frac{1}{2}} 2 = \log_{\frac{1}{2}} {(\frac{1}{2})}^{- 1} = - 1$

$f (4) = \log_{\frac{1}{2}} 4 = \log_{\frac{1}{2}} {(\frac{1}{2})}^{- 2} = - 2$

Zatvori

6.1 Logaritamska funkcija

Na početku...

Logaritam

Zadatak 1.

Zadatak 2.

Zadatak 3.

Zanimljivost

Zadatak 4.

Zadatak 5.

Dekadski logaritam

Zadatak 6.

Zadatak 7.

Prirodni logaritam

Zadatak 8.

Zanimljivost

Logaritamska funkcija

Kolekcija zadataka 1

Zadatak 9.

Zadatak 10.

...i na kraju

6.2 Graf i svojstva logaritamske funkcije