

Kut je dio ravnine određen s dva polupravca,
i
sa zajedničkim vrhom
. Oznaka:
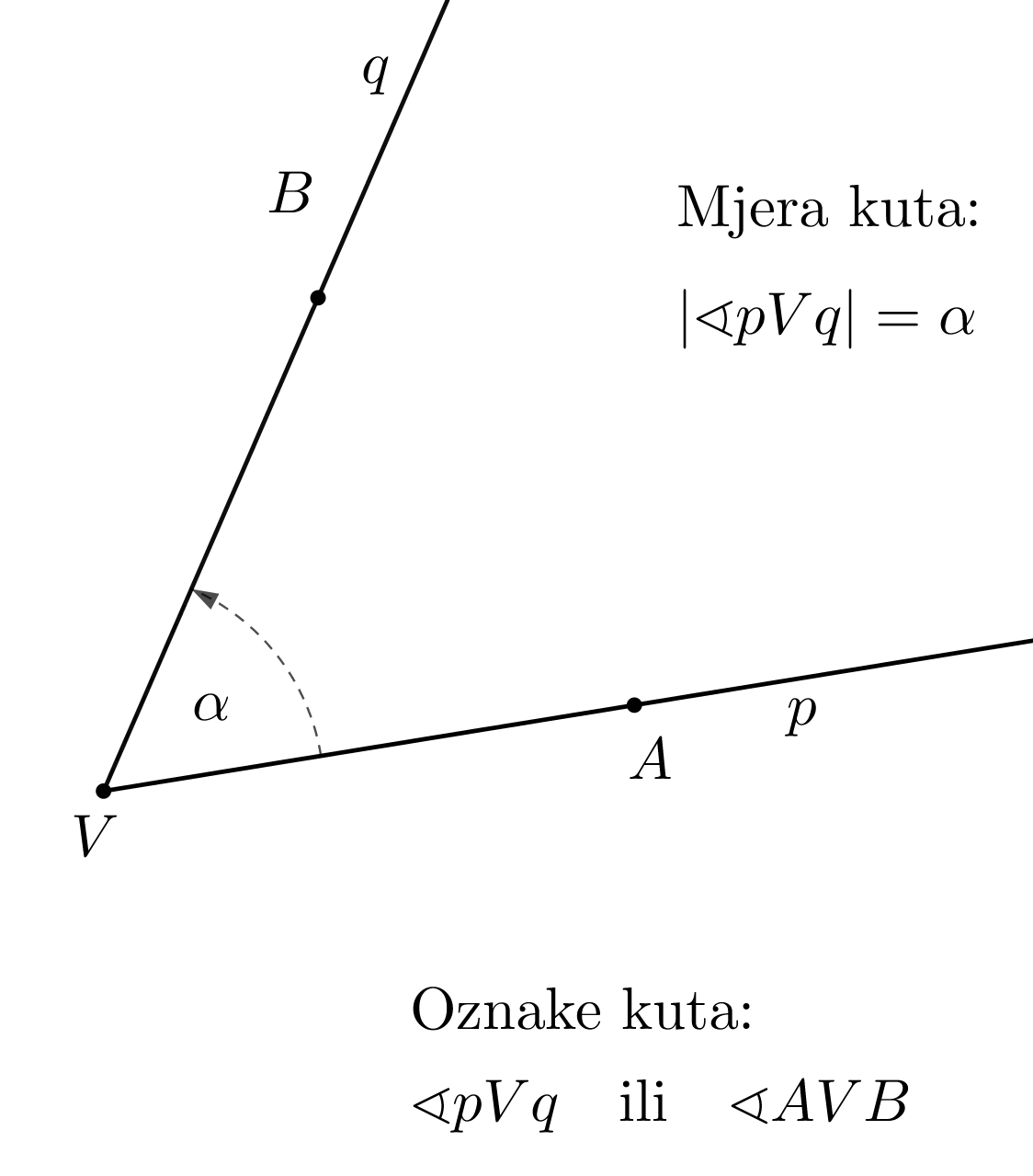
Ponovimo osnovne pojmove o kutu. Posložite zadane pojmove na pravo mjesto u tekstu.
Polupravac nazivamo
Pozitivan smjer za označavanje kuta jest u smjeru kazaljke na satu.
Osim stupnjeva i radijana postoji još jedna mjera kuta - gradijani.
U skladu s definicijom 1 stupnja, 1 grad (čitamo: jedan gradijan) jest
punog kuta ili
Jedinica je nastala u sklopu formiranja metričkog sustava 1793. godine u Francuskoj. U izradi metričkog sustava sudjelovao je i Jean-Charles de Borda (1733. - 1799.), francuski matematičar i fizičar. Imao je velik utjecaj na razvoj francuske flote. Izradio je logaritamsku tablicu trigonometrijskih funkcija u gradijanima u navigacijske svrhe. Ova mjerna jedinica nije uspjela opstati u odnosu na stupnjeve koji su bili dobro uspostavljeni i standardno korišteni već od kraja 18. stoljeća. Radijani su se koristili u teorijskoj matematici i znanosti.
Mjerne jedinice kuta
Mjerne jedinice kuta mogu biti radijan i stupanj.
STUPNJEVI
Ako se početna i završna zraka preklapaju, kažemo da zatvaraju kut od ili
. (čitamo: jedan stupanj) možemo definirati kao punog kuta.
RADIJANI
Radijan je veličina određena omjerom duljine luka kružnice sa središtem u vrhu kuta i polumjera te kružnice (čitamo: jedan radijan) jest kut kojemu je duljina luka jednaka polumjeru kružnog isječka kojim je kut definiran.
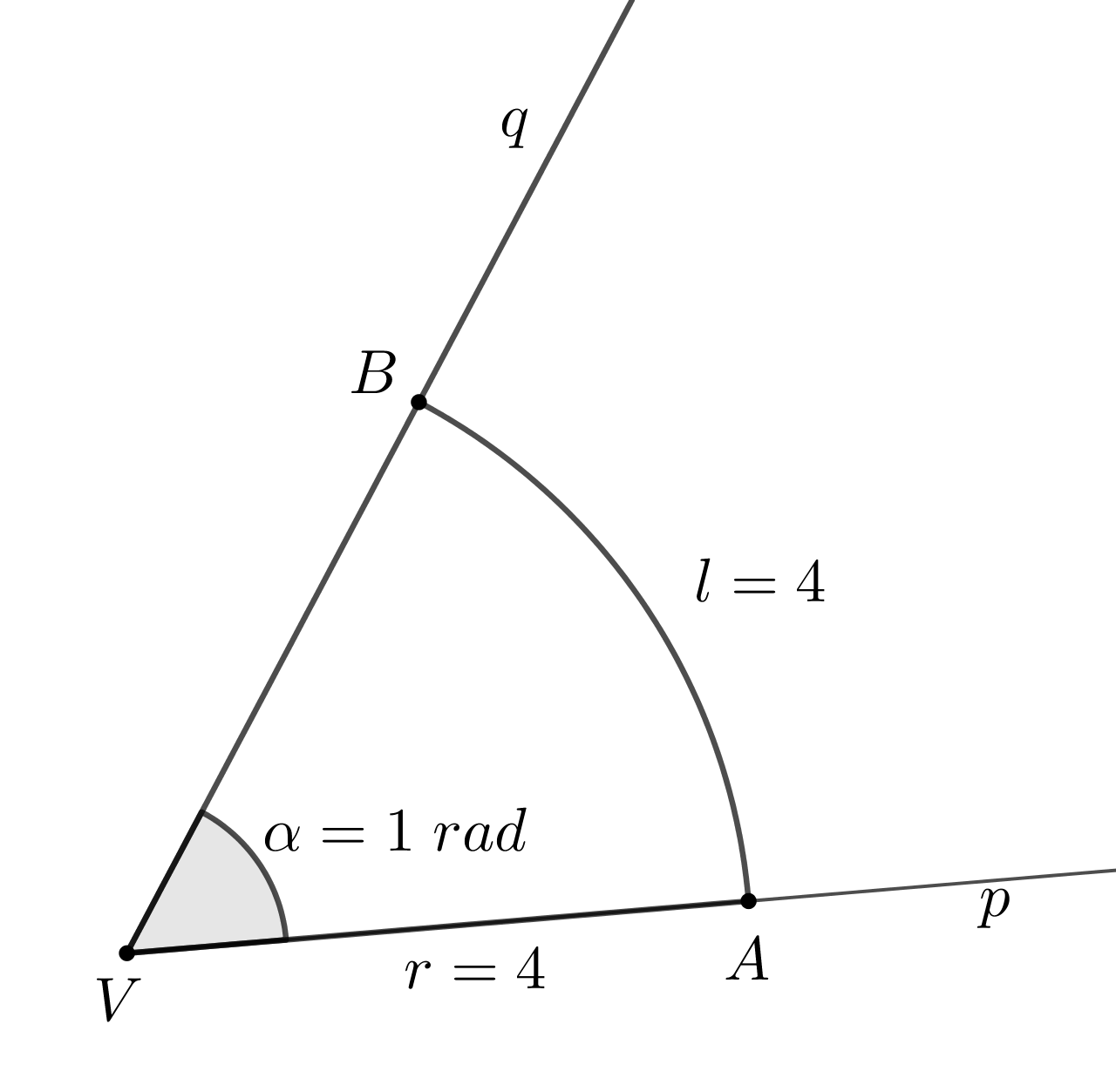
Pronađimo poveznicu između radijana i stupnjeva.
Nacrtajmo kružnicu polumjera Označimo s mjeru kuta i s duljinu pripadajućeg luka kružnice sa središtem u vrhu kuta.
Primjer 1.
- Odredimo mjeru kuta u radijanima.
- Odredimo mjeru kuta u stupnjevima.
Riješimo zadatak uvrštavanjem u prethodno dobivene formule za prijelaz iz stupnjeva u radijane množenjem stupnjeva s odnosno za prijelaz iz radijana u stupnjeve množenjem radijana sa
Obično rezultat ostavljamo u obliku razlomka i s brojem
ako postoji u rješenju. Rezultat u decimalnom obliku množimo s
.
Neka je zadana kružnica polumjera
(jedinična kružnica) čije je središte u ishodištu koordinatnog sustava.
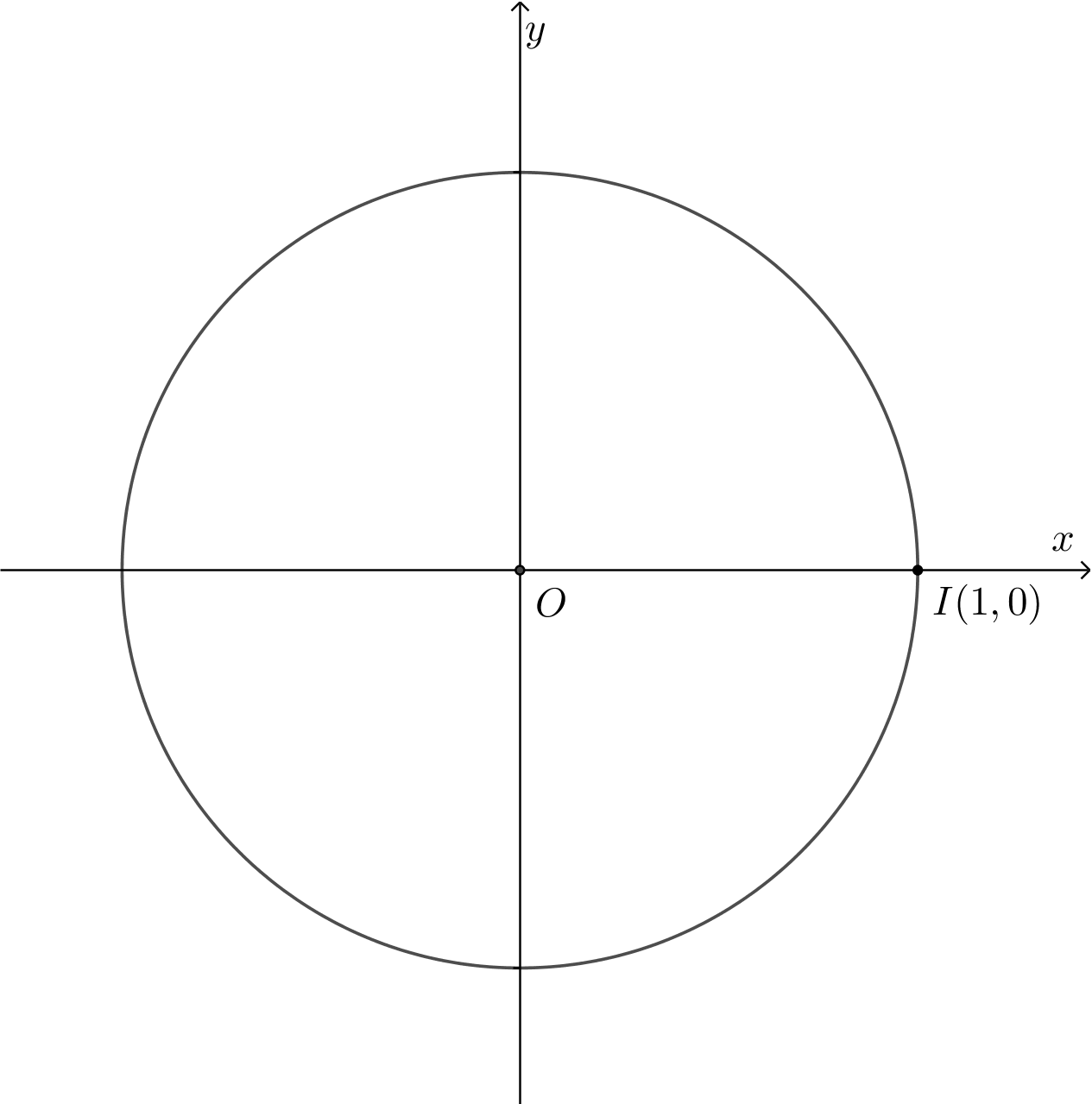
Smjestimo brojevni pravac okomito na os apscisu tako da ishodište bude u točki Pravac je tangenta kružnice.
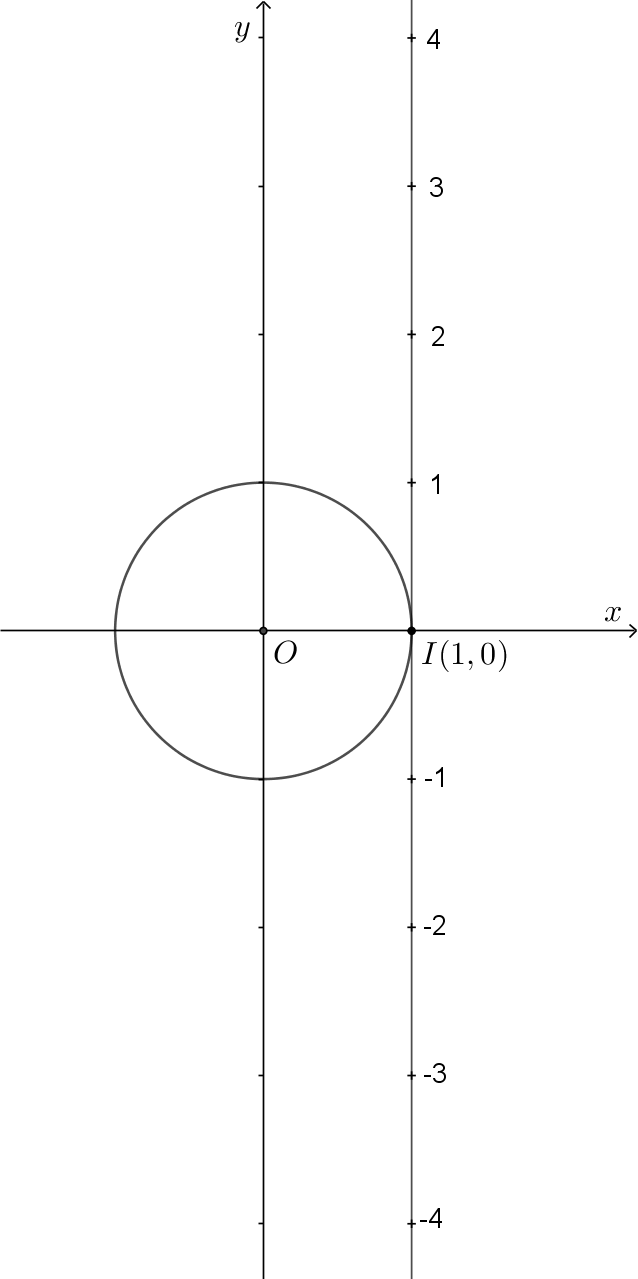
Namatajte pravac oko kružnice pomoću sljedeće interakcije. Razmislite što se događa s realnim brojevima na pravcu (prikazanim pomoću broja
). Možete li povezati točke na pravcu s točkama
na kružnici
(u ravnini)? U kakvoj su vezi mjera kuta u stupnjevima i realni broj s pravca?
Svaki realni broj s pravca pridružujemo nekoj točki na kružnici. Na taj smo način definirali novo preslikavanje s pravca na kružnicu.
Povežite mjeru kuta u stupnjevima s pripadajućom duljinom luka. Što je s mjerama kuta kada pravac namatamo u negativnom smjeru ili nakon prvoga punog kruga?
Preslikavanje koje realne brojeve
pridružuje točkama jedinične kružnice
nazivamo eksponencijalno preslikavanje:
Pokušajte napraviti sličnu simulaciju namatanja pravca oko kružnice. Budite kreativni, ali i strpljivi.
Potreban alat:
Pogledajte sljedeći video. Možda dobijete ideju kako izraditi kružnicu i pravac koji se namata oko kružnice.
Promatrajte što se događa s točkama nakon što jedanput prođemo cijelu kružnicu.
Pripremite sada brojevni pravac s realnim brojevima prikazanim pomoću broja
i namatajte ga oko kružnice.
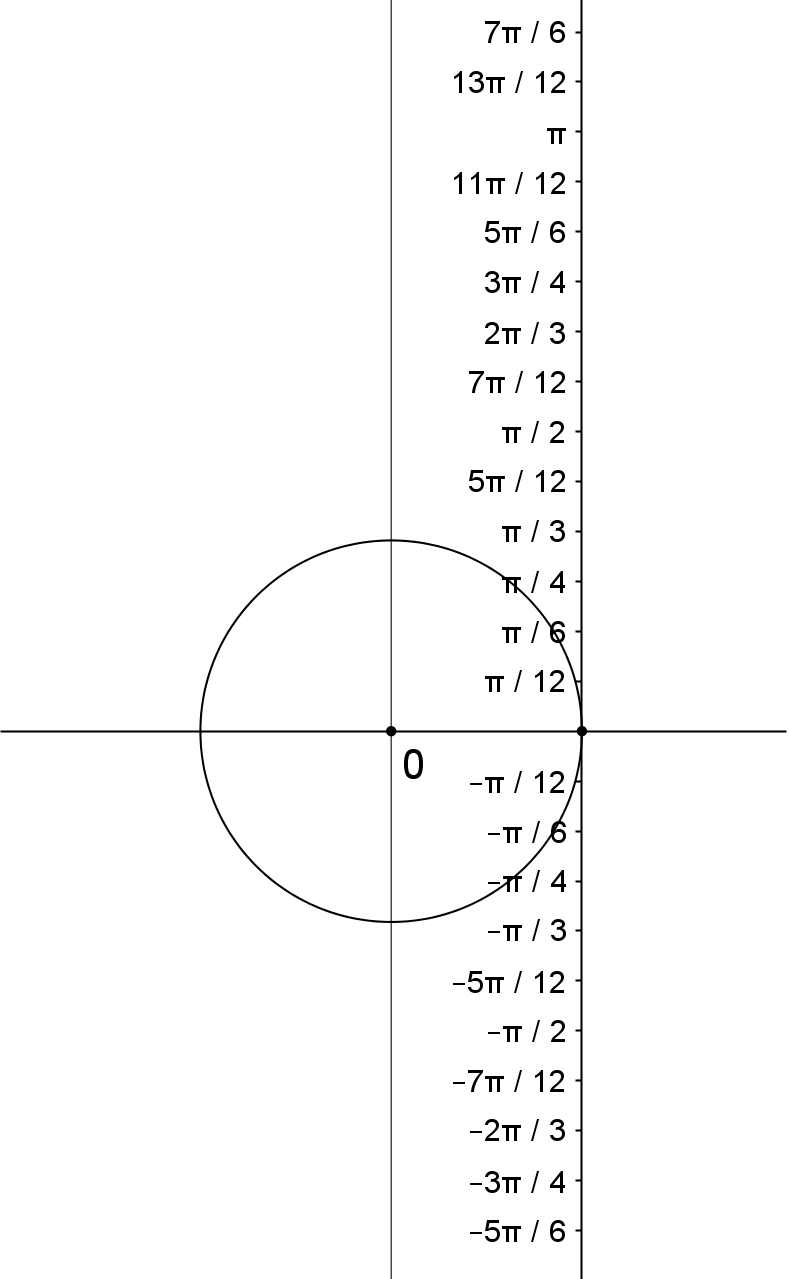
Kojim ćete točkama na kružnici pridružiti ovako zapisane realne brojeve?
Brojevna kružnica je jedinična kružnica čijim točkama eksponencijalnim preslikavanjem pridružujemo realne brojeve.
Primjer 2.
Kada bismo nastavili namatati pravac nakon punog kruga (dio pravca duljine ), točki kojoj smo u prvom krugu eksponencijalnim preslikavanjem pridružili broj sada bismo pridružili broj Dakle, vrijedi
Jednako tako, ako bismo namatali dio pravca s negativnim brojevima u smjeru kazaljke na satu, realan broj pridružili bismo istoj točki kojoj je pridružen broj , odnosno vrijedi
Odredite realne brojeve manje od
koji su pridruženi istoj točki kružnice kao i realni brojevi:
Prikažite ih na brojevnoj kružnici.
Dakle, radijanska mjera kuta
jest duljina luka kružnice od početne točke
do točke
na kružnici koja se dobije eksponencijalnim preslikavanjem
Naučili smo kako mjeri kuta pridružiti točku na kružnici.
Prisjetite se veze između radijanske mjere kuta i stupnjeva pa pokušajte pripadajuće vrijednosti u stupnjevima pridružiti točkama na kružnici.
Znamo da vrijedi
Primjer 3.
Koliko puta trebamo obići puni krug da bismo točki brojevne kružnice pridružili broj
Zadatak ćemo riješiti tako da izračunamo koliko puta ide u zadani broj. Pokušajmo s mješovitim brojem danog razlomka. Dijeljenjem s dobijemo s ostatkom. Budući da s nismo završili puni krug, rastavit ćemo razlomak na i ostatak.
Ovim smo računom dobili dvije informacije o broju.
- Namatali smo pravac 4 puna kruga dok nismo našli točku kojoj smo pridružili zadani broj.
- Vrijedi
Koliko puta trebamo obići puni krug da bismo točki brojevne kružnice pridružili broj
Dakle, na kružnici je u točki gdje i pravi kut nakon prolaska po cijeloj kružnici, tj.
Razvrstajte ponuđene brojeve ovisno koliko puta treba obići puni krug (pozitivan smjer kretanja), tj koliko puta treba dodati
broju iz intervala
kojoj pripada ista točka na kružnici.
U kojem su kvadrantu točke
i
Koliko punih krugova sadrže ove mjere i koja je pripadajuća mjera iz intervala
odnosno
Što primjećujete?
Mjera kuta
za koju vrijedi
ili
naziva se glavna mjera kuta.
Glavnu mjeru kuta dobijemo tako da mjeru kuta podijelimo s ili zatim najmanji cijeli broj rezultata toga dijeljenja označimo s i izračunamo:
ako se radi o radijanskoj mjeri kuta odnosno
ako se radi o mjeri kuta u stupnjevima.
Odredite glavne mjere kuta.
Dosadašnje znanje o kutovima u ravnini (od do ) proširili smo na kutove proizvoljne mjere, i pozitivne i negativne. Sada, kada znamo da mjera kuta može biti bilo koji realan broj koji lako pretvorimo u glavnu mjeru kuta, možemo definirati trigonometrijske funkcije na skupu realnih brojeva.
Budući da će vam za definiciju trigonometrijskih funkcija biti potrebno poznavanje brojevne kružnice te svođenje na glavnu mjeru kuta, provjerite jeste li te ishode dobro usvojili.
U sljedećoj interakciji za zadane realne brojeve najprije odredite pripadajuće glavne mjere kuta te ih potom smjestite na pravo mjesto na brojevnoj kružnici pomičući točke.