Povratak
U srednjoj ste se školi koristili različitim funkcijama. Prisjetimo se njihovih definicija i grafova.
Primjer 1.
Funkcije zadajemo domenom, kodomenom i pravilom pridruživanja. Crtamo graf funkcije i određujemo sliku. Pogledajte kako možemo odrediti domenu i sliku funkcije pomoću njezina grafa.
Riješite zadatke.
Funkciju
f:R→Rf:R→R s pravilom pridruživanja
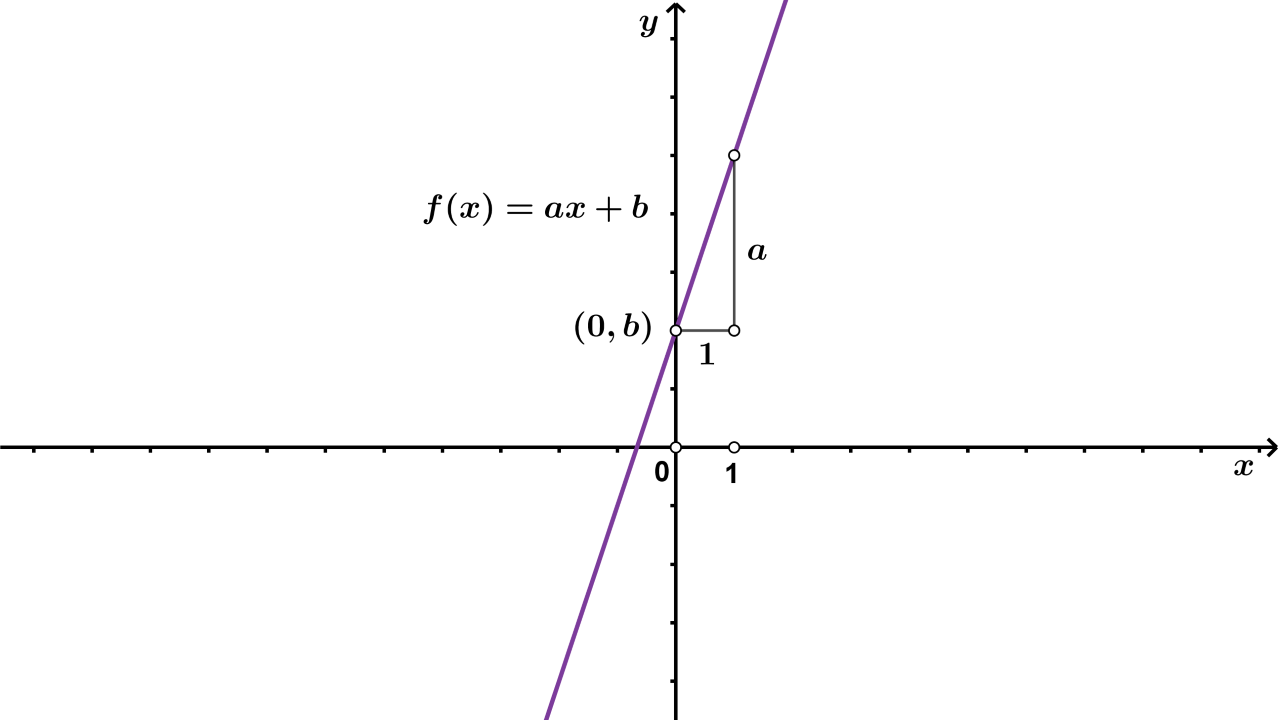
f(x)=ax+b,a,b∈R,a≠0f(x)=ax+b,a,b∈R,a≠0 zovemo linearna funkcija ili polinom prvog stupnja.
Funkciju g:R→Rg:R→R s pravilom pridruživanja g(x)=ax2+bx+c,a,b,c∈R,a≠0g(x)=ax2+bx+c,a,b,c∈R,a≠0 zovemo kvadratna funkcija ili polinom drugog stupnja.
Funkciju
h:R→Rh:R→R s pravilom pridruživanja
h(x)=anxn+an-1xn-1+...+a1x+a0,an,...,a0∈R,an≠0h(x)=anxn+an−1xn−1+...+a1x+a0,an,...,a0∈R,an≠0 zovemo polinom
n-n−tog stupnja.
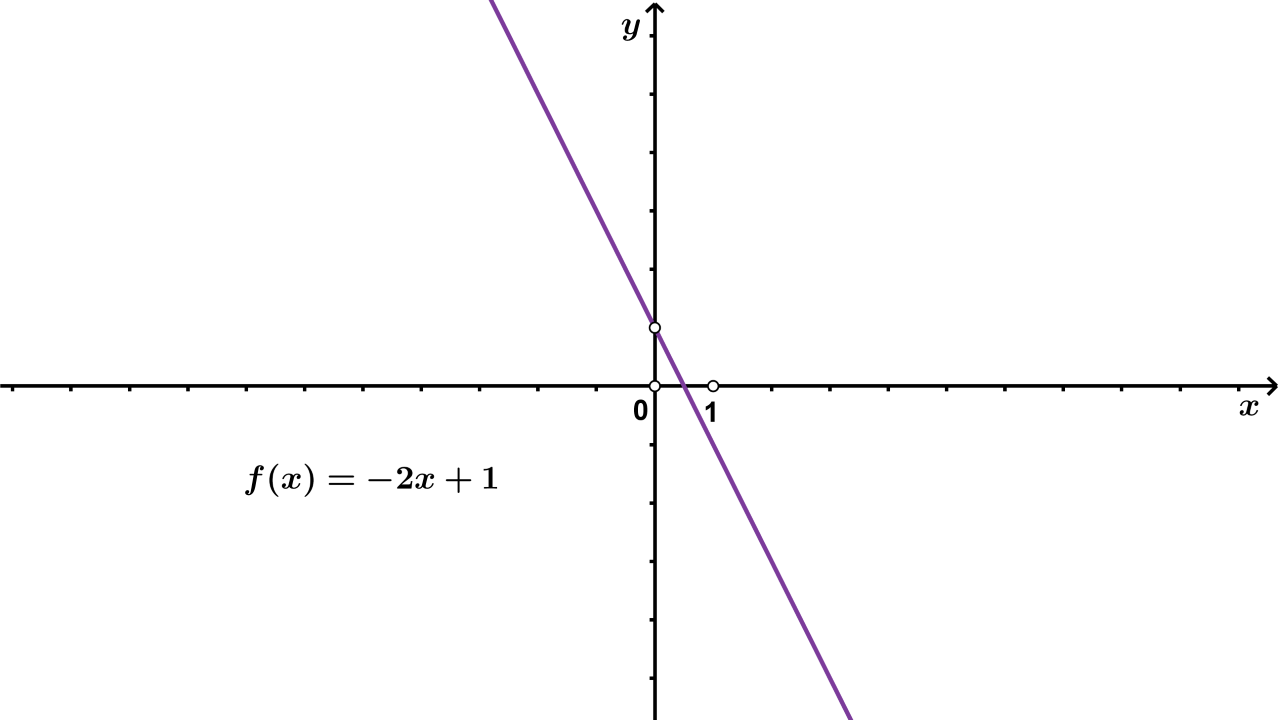
Graf linearne funkcije s pravilom pridruživanja f(x)=ax+bf(x)=ax+b je pravac. Koeficijent aa označava za koliko se promijeni vrijednost funkcije kad se xx poveća za jedan. Graf funkcije ff siječe os ordinata u točki (0,b).(0,b). Slika linearne funkcije je skup R.R.
Graf kvadratne funkcije s pravilom pridruživanja f(x)=ax2+bx+cf(x)=ax2+bx+c je parabola. Tjeme grafa točka je (x0,f(x0)),(x0,f(x0)), pri čemu je x0=-b2a.x0=−b2a. Slika kvadratne funkcije je skup [f(x0),∞⟩[f(x0),∞⟩ ako je a>0a>0 i ⟨-∞,f(x0)]⟨−∞,f(x0)] ako je a<0.a<0.
Nacrtajte u bilježnicu graf funkcije pa provjerite rješenje.
f(x)=-2x+1f(x)=−2x+1
f(x)=x2+2x-6f(x)=x2+2x−6
Za funkciju s pravilom pridruživanja
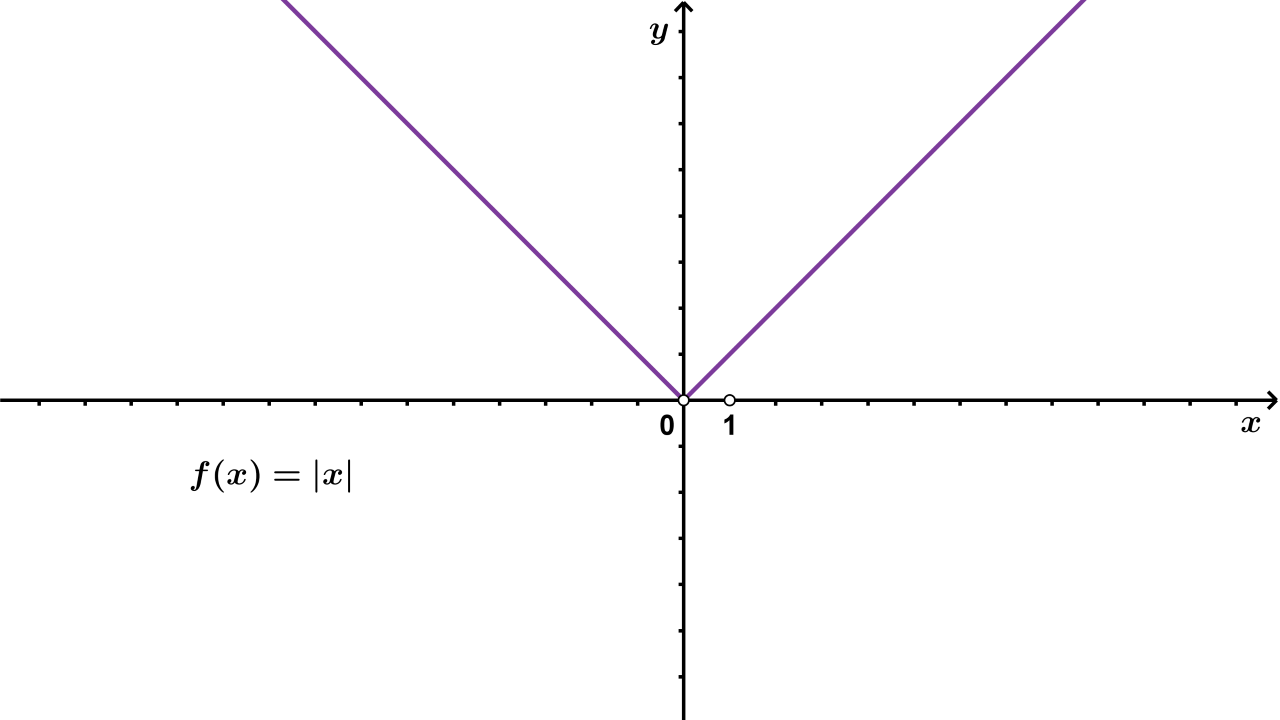
f(x)=|x|f(x)=|x| vrijedi:
Funkciju f:R→Rf:R→R s pravilom pridruživanja f(x)=|x|f(x)=|x| zovemo funkcija apsolutne vrijednosti.
Slika funkcije f(x)=|x|f(x)=|x| je skup [0,∞⟩.[0,∞⟩.
Za funkciju s pravilom pridruživanja
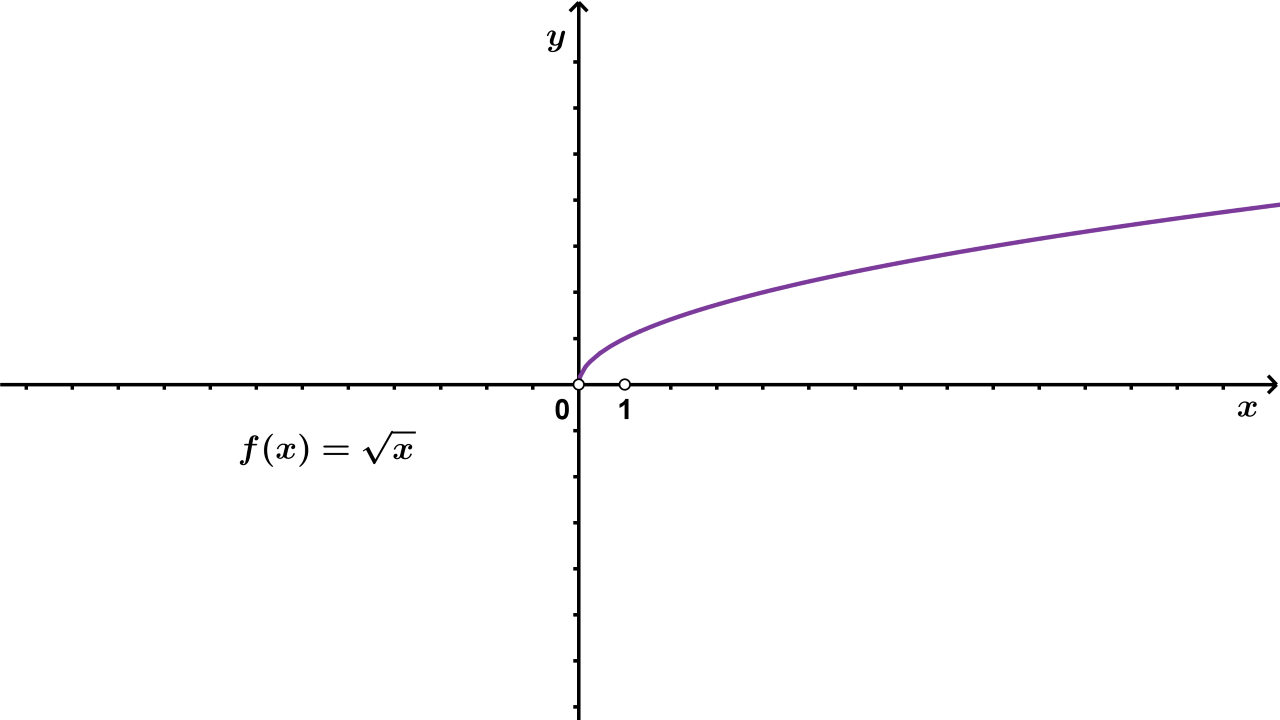
f(x)=√xf(x)=√x vrijedi:
Funkciju f:R+0→Rf:R+0→R s pravilom pridruživanja f(x)=√xf(x)=√x zovemo funkcija drugog korijena.
Slika funkcije f(x)=√xf(x)=√x je skup [0,∞⟩.[0,∞⟩.
Za funkciju s pravilom pridruživanja
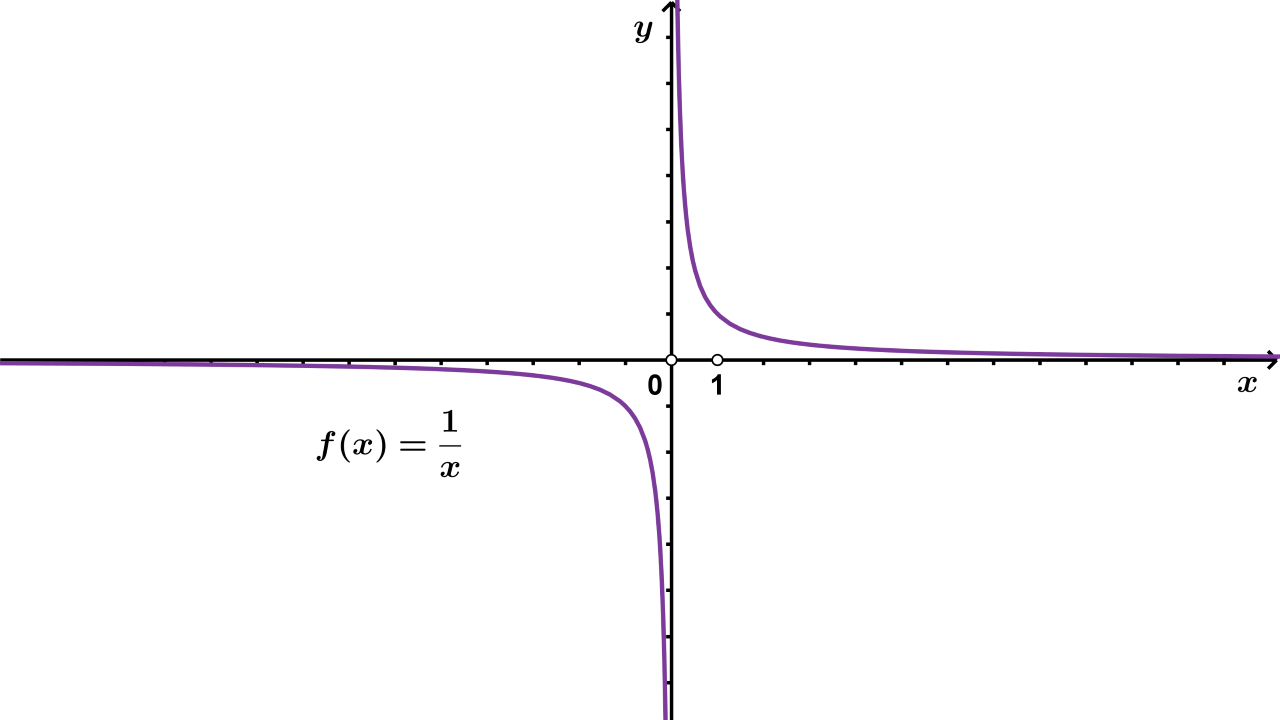
f(x)=1xf(x)=1x vrijedi:
Funkciju f:R\{0}→Rf:R\{0}→R s pravilom pridruživanja f(x)=1xf(x)=1x zovemo racionalna funkcija.
Slika racionalne funkcije f(x)=1xf(x)=1x je skup R\{0}.R\{0}.
Za funkciju s pravilom pridruživanja
f(x)=2xf(x)=2x vrijedi:
Za funkciju s pravilom pridruživanja
f(x)=log2xf(x)=log2x vrijedi:
Funkciju
f:R→R+f:R→R+ s pravilom pridruživanja
f(x)=ax,a>0,a≠1f(x)=ax,a>0,a≠1 zovemo eksponencijalna funkcija.
Funkciju
g:R+→Rg:R+→R s pravilom pridruživanja
g(x)=logax,a>0,a≠1g(x)=logax,a>0,a≠1 zovemo logaritamska funkcija.
Slika eksponencijalne funkcije f(x)=axf(x)=ax je skup R+.R+. Slika logaritamske funkcije g(x)=logaxg(x)=logax je skup R.R.
Funkcija s pravilom pridruživanja f(x)=sinxf(x)=sinx definirana je na skupu
Slika funkcija sinus, kosinus i tangens
Trigonometrijske funkcije sinus i kosinus definirane su na skupu RR
sin:R→R,sin:R→R, cos:R→R.cos:R→R. Slika je funkcije sinus i kosinus interval [-1,1].
Trigonometrijska funkcija tangens nije definirana za brojeve oblika π2+kπ,k∈Z
tg:R\{π2+kπ,k∈Z}→R. Slika funkcije tangens je skup R.
Povezujući elementarne funkcije računskim operacijama i promatrajući uzastopno djelovanje nekoliko elemenatarnih funkcija, dobit ćemo složene funkcije. Dobro poznavanje elementarnih funkcija, njihovih grafova i svojstava omogućit će rješavanje mnogih problema u matematici i primjeni.
Napravite mentalnu mapu u koju ćete upisati elementarne funkcije, njihove domene, kodomene, slike i grafove.
Uparite odgovarajuće elemente.
Označite graf linearne funkcije.
Na slici je prikazan graf funkcije
f(x)=0.5x.
Označite odgovore koji su točni za funkciju sinus.
Označite pravilo pridruživanja funkcije čiji je graf na slici.
